章节目录
- 个体与集成
- Boosting
- Bagging与随机森林
- 集合策略
- 多样性
(一)个体与集成
集成学习(ensemble learning)的一般结构:先产生一组“个体学习器”(individual learner),再用某种策略将他们结合起来,如下图所示,
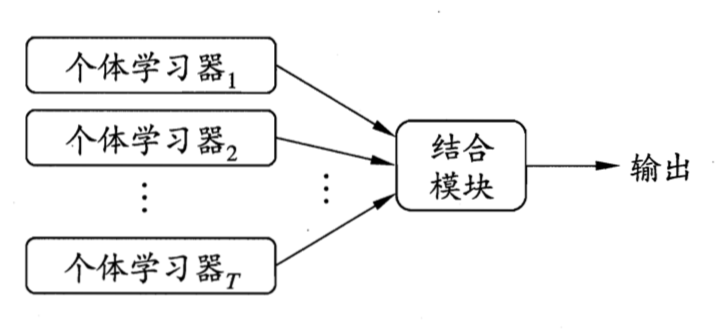
个体学习器通常由一个现有的学习算法从训练数据产生:
- 只包含同种类型的个体学习器,这样的集成是“同质”的(homogeneous)。同质集成中的个体学习器亦称为”基学习器“(base learning),相应的学习算法称为”基学习算法“(base learning algorithm)。
- 集成也可包含不同类型的个体学习器,这样集成是”异质“的(heterogeneous)。相应的个体学习器,常称为”组件学习器“(component learning)或直接称为个体学习器。
在一般的经验中,如果把好坏不等的东西掺到一起,那么通常结果会是比坏的好一些,比好的要坏一些。集成学习把多个学习器结合起来,如何能获得比最好的单一学习器更好的性能呢?
考虑一个简单的例子:在二分类任务中,假定三个分类器在三个测试样本的表现如下图所示,

其中,√表示分类正确,x表示分类错误,集成学习的结果通过投票法(voting)产生,即“少数服从多数”。这个简单的例子显示出:要获得好的集成,个体学习器应“好而不同”。个体学习器要有一定的“准确性”,即学习器不能太坏,而且要有“多样性”(diversity),即学习器之间有差异。事实上,如何产生并结合“好而不同”的个体学习器,恰是集成学习研究的核心。
根据个体学习器的生成方式,目前集成学习的方法大致可分为两大类:
- 个体学习器间存在强依赖关系、必须串行生成的序列化方法,代表是Boosting;
- 个体学习器间不存在强依赖关系、可同时生成的并行化方法,代表是Baggig和“随机森林”(Random Forest);
(二)Boosting
Boosting是一族可将弱学习器提升为强学习器的算法。这族算法的工作机制类似:先从初始训练集训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续收到更多的关注,然后基于调整后的样本分布来训练下一个基学习器;如此重复进行,直到基学习器数目达到事先指定的值T,最终将这T个学习器进行加权结合。
Boosting族算法最著名的代表是AdaBoost。AdaBoost有多种推导方式,比较容易理解的是基于“加性模型”(additive model)即基学习器线性组合,

来最小化指数损失函数(exponential loss function):

boosting中的Adaboost算法的详细推导过程——P172:略复杂,有空再看。
(三)Bagging与随机森林
欲得到泛化性能强的集成,集成中的个体学习器应尽可能独立。虽然“独立”在显示任务中无法做到,但可以设法使基学习器尽可能具有较大差异。给定一个训练数据集,一种可能的做法是对训练样本进行采样,产生若干个不同的子集,再从每个数据子集中训练出一个基学习器。这样,由于训练数据不同,我们获得的基学习器可望具有比较大的差异。然而,为获得更好的集成,我们还同时希望个体学习器不能太差。如果采样出的每个子集都完全不同,则每个基学习器只用到了一小部分训练数据,甚至不足进行有效学习,这显然无法确保产生出比较好的基学习器。为考虑这个问题,我们可考虑使用相互有交叠的采样子集。
1. Bagging
Bagging是并行式集成学习方法最著名的代表,从名字即可看出,它直接基于前面介绍过的自助采样法(bootstrap sampling)。
从偏差-方差分解角度看,Bagging主要关注降低方差。
2. 随机森林
随机森林(Random Forest,简称RF)是Bagging的一个扩展变体。RF在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机属性选择。
随机森林对Bagging只做了小改动,但是与Bagging中基学习器的“多样性”仅通过样本扰动(通过对初始训练集采样)而来不同,随机森林中基学习器多样性不仅来自样本扰动,还来自属性扰动,这就使得最终集成的泛化性能可通过个体学习器之间的差异度的增加而进一步提升。
(四)组合策略
学习器结合可能从三个方面带来好处:
- 从统计的方面看,由于学习任务的假设空间往往很大,可能有多个假设在训练集上达到同等性能,此时若使用单学习器可能因误选而导致泛化性能不佳,结合多个学习器减小这一风险;
- 从计算的方面来看,学习算法往往会陷入局部极小,有的局部极小点所对应的泛化性能可能很糟,而通过多次运行之后进行结合,可降低陷入糟糕局部极小点的风险;
- 从表示的方面来看,某些但学习器则肯定无效,而通过结合多个学习器,由于响应的假设空间有所扩大,有可能学得更好的近似。
直观的示意图如下所示:
集成学习常见策略有:
- 平均法:简单平均法和加权平均法。
- 投票法:绝对多数投票法;相对多数投票法;加权投票法
- 学习法:初级学习器+次级学习器
(五)多样性
误差-分歧分解
欲构建泛化能力强的集成,个体学习器应“好而不同”,其中,“误差-分歧分解”(error-ambiguity decomposition)是一个简单的理论分析方法。但该推导过程只适用于回归学习,难以直接推广到分类学习任务中。
多样性度量
多样性度量(diversity measure)是用于度量集成中个体分类器的多样性,即估算个体学习器的多样化程度。常用的多样性度量包括:
- 不合度量(disagreement measure)
- 相关系数(correlation coefficient)
- Q-统计量(Q-statistics)
- k-统计量(k-statistics)
多样性增强
在集成学习中需有效地生成多样性大的个体学习器。与简单地直接用初始数据训练出个体学习器相比,一般思路是在学习过程中引入随机性,常见的做法主要有,
- 数据样本扰动:数据样本扰动基于采样法。
- 输入属性扰动:随机子空间算法。
- 输出表示扰动:翻转法(随机改变一些训练样本的标记);输出调制法(将分类输出转化为回归输出后构建学习器)…
- 算法参数扰动:负相关法;单一学习器通常需要交叉验证等来确定参数值。
参考资料
- 西瓜书《机器学习》
- 《机器学习》笔记-集成学习(8)



