算法导论详解(6) 第七章快速排序

快速排序简介

快排最坏情况$O( n^2 )$，但平均效率$O(n lg n)$，而且$O(n lg n)$隐含的常数因子很小，快排可以说是最快的排序算法，并非浪得虚名。另外它还是原址排序。

快速排序是基于分治模式的：

分解：数组A【p..r】被划分成两个（可能空）子数组A【p..q-1】和A【q+1..r】，使得A【p..q-1】中的每个元素都小于等于A(q)，而且，小于等于A【q+1..r】中的元素。计算下标q也是划分过程中的一部分。
解决：通过递归调用快速排序，对子数组A【p..q-1】和A【q+1..r】排序。
合并：因为两个子数组是原址排序的，将它们的合并不需要操作：整个数组A【p..r】已排序。

快排的伪码：

其中对数组的划分：Partition是快排算法的关键，，它对子数组A【p..r】进行原址重排）。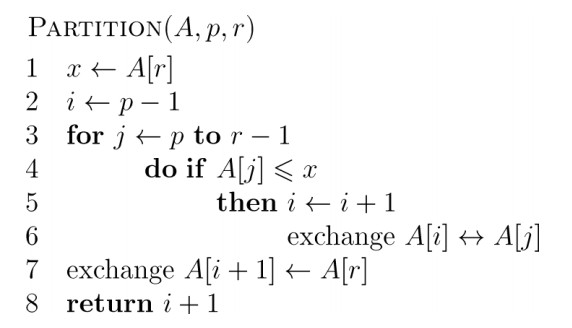

快速排序Python实现

def PARTITION(A, p, r):
    x = A[r]
    i = p - 1
    for j in range(p, r):  # not r-1, but r
        if A[j] < x:
            i = i + 1
            A[i], A[j] = A[j], A[i]
    A[r], A[i + 1] = A[i + 1], A[r]
    return i + 1
def QUICKSORT(A, p, r):
    if p < r:
        q = PARTITION(A, p, r)
        QUICKSORT(A, p, q - 1)
        QUICKSORT(A, q + 1, r)
if __name__ == "__main__":
    A = [2, 8, 7, 1, 3, 5, 6, 4]
    QUICKSORT(A, 0, len(A) - 1)  # all start from 0
    for i in range(0, len(A)):
        print(A[i], end="  ")

快速排序性能分析

当数据量很小的时候，大概就十来个元素的小型序列，快排的优势并不明显，甚至比插入排序慢。但是一旦数据多，它的优势就充分发挥出来了。

举一个例子，C++ STL 中的sort函数，就充分发挥了快排的优势，并且取长补短，在数据量大时采用QuickSort，分段递归排序。一旦分段后的数据量小于某个门槛，为避免QuickSort递归调用带来过大的额外负荷，就改用插入排序。如果递归层次过深，还会改用HeapSort(堆排序，第六章刚讲)。所以说，C++的“混合兵种”sort的性能肯定会比C的qsort好。

快排的运行时间与Partition的划分有关：

最坏情况是输入的数组已经完全排好序，那么每次划分的左、右两个区域分别为n-1和0，效率为$O( n^2 )$.
而对于其他常数比例划分，哪怕是左右按9:1的比例划分，效果都是和在正中间划分一样快的（算法导论上有详细分析）
即，任何一种按照常数比例进行划分，总运行时间都是$\text{O}(n \text{lg} n)$。

快速排序的随机化版本

随机抽样(random sampling):从$A[p..r]$中随机选一个元素作为主元，而不是始终采用$A[r]$作为主元。

随机化的快排的伪码如下：

快速排序的随机化版本

Python实现：

import random
def PARTITION(A, p, r):
    x = A[r]
    i = p - 1
    for j in range(p, r):  # not r-1, but r
        if A[j] < x:
            i = i + 1
            A[i], A[j] = A[j], A[i]
    A[r], A[i + 1] = A[i + 1], A[r]
    return i + 1
def RANDOMIZED_PARTITION(A, p, r):
    rand_i = random.random()
    # print(round(a *(r - p)) + p)
    rand_i = round(rand_i * (r - p) + p)  # 区间的计算需要注意，否则不对
    A[rand_i], A[r] = A[r], A[rand_i]
    return PARTITION(A, p, r)
def RANDOMIZED_QUICKSORT(A, p, r):
    if p < r:
        q = RANDOMIZED_PARTITION(A, p, r)
        RANDOMIZED_QUICKSORT(A, p, q - 1)
        RANDOMIZED_QUICKSORT(A, q + 1, r)
if __name__ == "__main__":
    A = [2, 8, 7, 1, 3, 5, 6, 4]
    RANDOMIZED_QUICKSORT(A, 0, len(A) - 1)  # all start from 0
    for i in range(0, len(A)):
        print(A[i], end="  ")

快速排序简介

快速排序Python实现

快速排序性能分析

快速排序的随机化版本

参考