Fork me on GitHub

算法导论详解(5) 第六章 堆排序

发表于 | 分类于 | 阅读次数:
字数统计: 1,544

在第二章介绍了两种排序算法，第六章将介绍第三种排序算法：堆排序(heapsort)，以及基于堆排序的优先队列。

空间原址性(in place)：仅有常数个元素需要在排序过程中存储在数组之外。

堆(6.1, P84)

堆，也叫 二叉堆，是一个数组，可以看作近似的完全二叉树，树的每个节点对应数组一个元素。

表示堆的数组A包括两个属性：A.length给出数组元素的个数；A.heap-size给出有多少个元素存储在该数组中。即heap-size是数组的有效元素。

给定下标i，很容易计算其父节点、左节点和右节点：

1
2
3
4
5
6
def PARENT(i):
    return i / 2
def LEFT(i):
    return 2 * i
def RIGHT(i):
    return 2 * i + 1

这三个函数通常以宏或者内联函数的方式实现。

二叉堆分为两种形式：最大堆和最小堆。
最大堆满足：A[PARENT(i)] ≥ A[i] ，即：某个节点的值最多与其父节点一样大；最小堆满足：A[PARENT(i)] ≤ A[i]。

堆排序算法采用的是最大堆。最小堆通常用于构造优先队列。

堆的高度为：$Θ(lgn)$

维持堆的性质（6.2，P86）

MAX-HEAPIFY：输入为一个数组A和一个下标i，A[i]有可能小于其孩子，通过让A[i]在数组中“逐级下降”，从而使得以下标i为根节点的子树重新遵循最大堆的性质。

该函数伪码表示为：
MAX-HEAPIFY伪码

算法图示：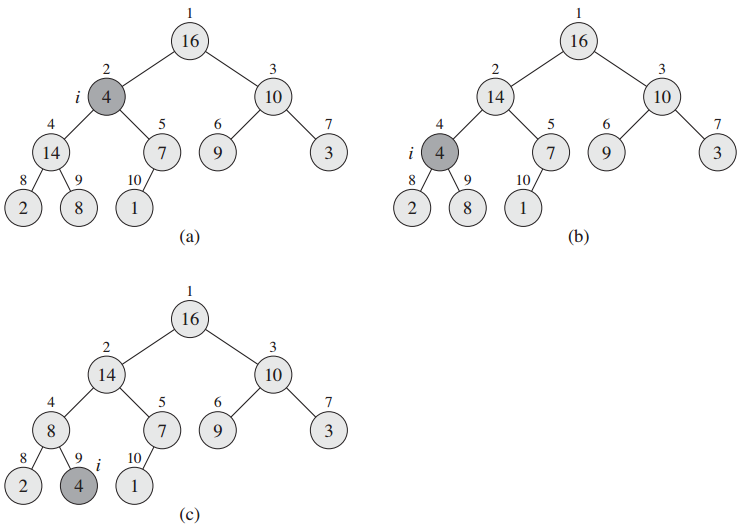

Python实现为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def MAX_HEAPIFY(A, i):
    l = LEFT(i)
    r = RIGHT(i)
    largest = -1
    if l <= len(A) and A[l - 1] > A[i - 1]:
        largest = l
    else:
        largest = i
    if r <= len(A) and A[r - 1] > A[largest - 1]:
        largest = r
    if largest != i:
        A[i - 1], A[largest - 1] = A[largest - 1], A[i - 1]
        MAX_HEAPIFY(A, largest)

每个孩子的子树最多为2n/3（不太理解这句话？？）。
所以，在最差情况下（最底层恰好半满）运行时间为：
$$T(n) = T(2n/3)+ \Theta(1)$$
上述递归式的解为：$T(n) = \text{O} (\text{lg}n)$

建堆(6.3, P87)

子数组元素$A[ (\lfloor n/2\rfloor +1),\cdots,n]$是树中的所有叶节点。
BUILD_MAX_HEAP从非叶节点开始一直循环到根节点。

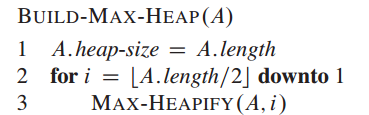
Python实现为：

1
2
3
4
5
from math import floor
def BUILD_MAX_HEAP(A):
    heap_size = len(A)
    for i in range(int(floor(heap_size / 2)), 0, -1):
        MAX_HEAPIFY(A, i)

BUILD_MAX_HEAP 的时间复杂度为$T(n) = \text{O}(n)$

堆排序算法(6.4，P89)

伪代码：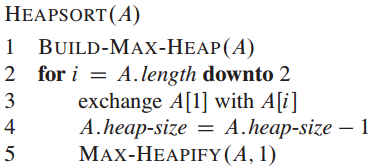

Python实现：

1
2
3
4
5
6
7
def HEAPSORT(A):
    BUILD_MAX_HEAP(A)
    heap_size = len(A)
    for i in range(len(A), 1, -1):
        A[1 - 1], A[i - 1] = A[i - 1], A[1 - 1]  # exchage A[i] with A[1]
        heap_size = heap_size - 1
        MAX_HEAPIFY(A, 1, heap_size)

HEAPSORT过程的时间复杂度为：$\text{O}(n\text{lg}n)$，因为BUILD_MAX_HEAP的时间复杂度为$\text{O}(n)$，n-1次调用MAX_HEAPIFY，每次时间为$\text{O}(\text{lg}n)$。

堆排序的Python完整实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
from math import floor
def PARENT(i):
    return i / 2
def LEFT(i):
    return 2 * i
def RIGHT(i):
    return 2 * i + 1
def MAX_HEAPIFY(A, i, size):
    l = LEFT(i)
    r = RIGHT(i)
    largest = -1
    if l <= size and A[l - 1] > A[i - 1]:
        largest = l
    else:
        largest = i
    if r <= size and A[r - 1] > A[largest - 1]:
        largest = r
    if largest != i:
        A[i - 1], A[largest - 1] = A[largest - 1], A[i - 1]
        MAX_HEAPIFY(A, largest, size)
        
def BUILD_MAX_HEAP(A):
    heap_size = len(A)
    for i in range(int(floor(heap_size / 2)), 0, -1):
        MAX_HEAPIFY(A, i, heap_size)
        
def HEAPSORT(A):
    BUILD_MAX_HEAP(A)
    heap_size = len(A)
    for i in range(len(A), 1, -1):
        A[1 - 1], A[i - 1] = A[i - 1], A[1 - 1]  # exchage A[i] with A[1]
        heap_size = heap_size - 1
        MAX_HEAPIFY(A, 1, heap_size)
if __name__ == "__main__":
    # A = [16, 4, 10, 14, 7, 9, 3, 2, 8, 1]
    # MAX_HEAPIFY(A, 2)
    # for i in range(0, len(A)):
    #     print(A[i], end=" ")
    # A = [4, 1, 3, 2, 16, 9, 10, 14, 8, 7]
    # BUILD_MAX_HEAP(A)
    # for i in range(0, len(A)):
    #     print(A[i], end=" ")
    A = [4, 1, 3, 2, 16, 9, 10, 14, 8, 7]
    HEAPSORT(A)
    for i in range(0, len(A)):
        print(A[i], end=" ")

优先队列(6.5，P90)

优先队列：是一种用来维护由一组元素构成的集合S的数据结果，其中的每个元素都有一个相关的值，称为关键字。优先队列也有两种形式：最大优先队列和最小优先队列。

最大优先队列的应用：共享计算机系统的作业调度。
最小优先队列被用于基于事件驱动的模拟器。队列中保存要模拟的事件，每个事件都有一个发生事件作为关键词。

优先队列可以用堆来实现。优先队列的元素对应应用程序的对象，堆中每个元素存储对象的句柄(handle)。

最大优先队列支持：

  • 对最大优先队列进行插入，MaxHeapInsert；
  • 返回最大优先队列的最大值，HeapMax；
  • 去掉最大值并且返回该值，HeapExtractMax；
  • 将第x个元素的值改为k，其中k>=x的原来的值，HeapIncreaseKey；
1
2
3
4
5
6
7
8
9
10
11
12
def HEAP_MAXIMUM(A):
    return A[1]
def HEAP_EXTRACT_MAX(A, heap_size):
    if heap_size < 1:
        print("ERROR!! Heap underflow!!")
        return -1
    max_A = A[1 - 1]
    A[1 - 1] = A[heap_size - 1]
    heap_size = heap_size - 1
    MAX_HEAPIFY(A, 1, heap_size)
    return max_A

HeapExtractMax的操作复杂度为$\text{O}(\text{lg}n)$（也就是MAX_HEAPIFY的复杂度）。

最大优先队列的Python完整实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
def PARENT(i):
    return i / 2
def LEFT(i):
    return 2 * i
def RIGHT(i):
    return 2 * i + 1
def MAX_HEAPIFY(A, i, heap_size):
    l = LEFT(i)
    r = RIGHT(i)
    largest = -1
    if l <= heap_size and A[l - 1] > A[i - 1]:
        largest = l
    else:
        largest = i
    if r <= heap_size and A[r - 1] > A[largest - 1]:
        largest = r
    if largest != i:
        A[i - 1], A[largest - 1] = A[largest - 1], A[i - 1]
        MAX_HEAPIFY(A, largest, heap_size)
def HEAP_MAXIMUM(A):
    return A[1]
def HEAP_EXTRACT_MAX(A, heap_size):
    if heap_size < 1:
        print("ERROR!! Heap underflow!!")
        return -1
    max_A = A[1 - 1]
    A[1 - 1] = A[heap_size - 1]
    heap_size = heap_size - 1
    MAX_HEAPIFY(A, 1, heap_size)
    return max_A
def HEAP_INCREASE_KEY(A, i, key):
    if key < A[i - 1]:
        print("ERROR!! New key is smaller than current key!!!")
        return
    A[i - 1] = key
    while i > 1 and A[int(PARENT(i) - 1)] < A[int(i - 1)]:
        A[int(PARENT(i) - 1)], A[int(i - 1)] = A[int(i - 1)], A[int(PARENT(i) - 1)]
        i = PARENT(i)
def MAX_HEAP_INSERT(A, key):
    MAX_INT = 0x7fffffff
    heap_size = len(A) + 1
    A.append(- MAX_INT)  # 尾部追加元素
    HEAP_INCREASE_KEY(A, heap_size, key)
if __name__ == "__main__":
    A = [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
    MAX_HEAP_INSERT(A, 9)  # 调用的数值都是从1开始。
    for i in range(0, len(A)):
        print(A[i], end=" ")

算法基本思想：在末尾新插入一个元素，按照最大堆的要求排列好就行。

参考资料

------ 本文结束感谢您的阅读 ------
坚持原创技术分享，您的支持将鼓励我继续创作！
分享到： 收藏夹 复制网址 邮件 微信 QQ空间 腾讯微博 豆瓣 一键分享 更多