本文介绍了BP网络中的前向传播和反向传播过程的公式与推导,读者可自行揣摩。
mathjax公式中不能有多余的{},否则
hexo deploy的时候会出现错误。
网络结构参数说明
BP神经网络示意图

注意,上述层与层之间是全连接的,示意图并没有画全。
网络结构
一个输入层,两个隐含层,一个输出层。
参数标记
输入层神经元个数n、输出层神经元个数m
两个隐含层神经元个数均为100
- 权值:输入层与第一个隐含层之间的权值为$w_{ij}$,两个隐含层之间的权值为$w_{jk}$,第二个隐含层与输出层之间的权值为$w_{kl}$
- 阈值:两个隐含层$a^1_j,a^2_k$,输出层$b_l$
其中,$i=1,2,…,n$,$j,k=1,2,…,100$,$l=1,2,…,m$
凡是下标含有$i,j,k,l$的,均表示单个神经元。
BP网络推导
前向传播
两个隐含层及输出层的输出:
$$H_j^1 = f(\sum_{i=1}^n w_{ij} x_i - a_{j}^1 )\ \ \ j=1,2,…,100$$
$$
H_{k}^2 = f(\sum^{100}_{j=1} w_{jk} H^1_{j} - a^2_{k} )\ \ \ k = 1,2, \cdots ,100
$$
$$
O_l = \sum_{k = 1}^{100} w_{kl}H_{k}^2 - {b_l} \ \ \ l = 1,2, \cdots ,m
$$
误差
此处仅仅是简单相减,可以使用MSE均方误差,有空改。
$$e_l = y_l - O_l\ \ \ l = 1,2, \cdots ,m$$
其中,$y_l$是真实的样本输出。
反向传播的权值更新
$$\begin{equation}\begin{split}
w_{kl} &= w_{kl} - dw_{kl} \\
&= w_{kl} - \eta \frac{\partial e_l}{\partial w_{kl}}\\
&= w_{kl} + \eta H_k^2 e_l \ \ \ \ \ \ k = 1,2, \cdots ,100 \\
\end{split}\end{equation}$$
$$\begin{equation}\begin{split}
{w_{jk}} &= {w_{jk}} - \eta \frac{\partial e_l}{\partial w_{jk}} \\
&= {w_{jk}} - \eta \frac{\partial e_l}{\partial O_l} \frac{\partial O_l}{\partial H_{k}^2} \frac{\partial H_{k}^2}{\partial w_{jk}} \\
&= {w_{jk}} - \eta (-e_l)(\sum_{l = 1}^m w_{kl}) (f’_{H_k^2} H_j^1) \\
&= {w_{jk}} + \eta f’_{H_k^2} H_j^1 \sum_{l = 1}^m w_{kl}e_l \ \ \ \ \ j = 1,2, \cdots ,100 \\
\end{split}\end{equation}$$
$$\begin{equation}\begin{split}
{w_{ij}} &= {w_{ij}} - \eta \frac{\partial e_l}{\partial w_{ij}} \\
&= {w_{jk}} - \eta \frac{\partial e_l}{\partial O_l} \frac{\partial O_l}{\partial H_{k}^2} \frac{\partial H_{k}^2}{\partial H_{j}^1} \frac{\partial H_{j}^1}{\partial w_{ij}} \\
&= {w_{jk}} - \eta (-e_l)(\sum_{l = 1}^m w_{kl}) (f’_{H_k^2} \sum_{k = 1}^{100} w_{jk}) (f’_{H_j^1} x_i) \\
&= {w_{ij}} + \eta f’_{H_j^1}{x_i}\sum_{k = 1}^{100} [(\sum_{l = 1}^m w_{kl}e_l)w_{jk}f’_{H_k^2}] \\
\ \ \ \ &其中 i = 1,2, \cdots ,n;j = 1,2, \cdots ,100 \\
\end{split}\end{equation}$$
这边公式需要自己推一推啦,详细地说明暂时就不多说。
还可以简写。有空补。
关于激活函数的说明
上述公式中,$f’_{H_k^2}$, $f’_{H_j^1}$ 之所以没有代入具体值,是因为这取决与所采用的激活函数。DeepLearnToolBox之BP算法中可采用的激活函数有两种,一是sigmoid函数,二是双曲正切函数。
sigmoid函数
当激活函数为sigmoid函数$f(x) = \frac{1} { 1 + e^{-x} }$时,sigmoid函数的导数具有下面的一个性质:
其导数为:
$$\begin{equation}\begin{split}
f’(x) &= \frac{e^{ - x}}{(1 + e^{ - x})^2} \\
&= \frac{e^{ - x}}{(1 + e^{ - x})}\frac{1}{(1 + e^{ - x})}\\
&= (1 - \frac{1}{(1 + e^{-x})})(\frac{1}{(1 + e^{ - x})}) \\
&= (1-f(x))f(x)\\
\end{split}\end{equation}$$
因此,比如说,在$H^2_K$中对$f$求导,结果为$f’_{H_k^2} = H_k^2(1-H_k^2)$,同理$f’_{H_k^1} = H_k^1(1-H_k^1)$
tanh函数
激活函数也可以是双曲正切函数$tanhx= \frac{sinhx}{coshx} = \frac{e^x-e^{-x}}{e^x+e^{-x}}$。
双曲正切函数的图形夹在水平直线y=1及y=-1之间,且当x的绝对值很大时,它的图形在第一象限内接近于直线y=1,而在第三象限内接近于直线y=-1。[1]
即双曲正切函数的值域是(-1,1)。
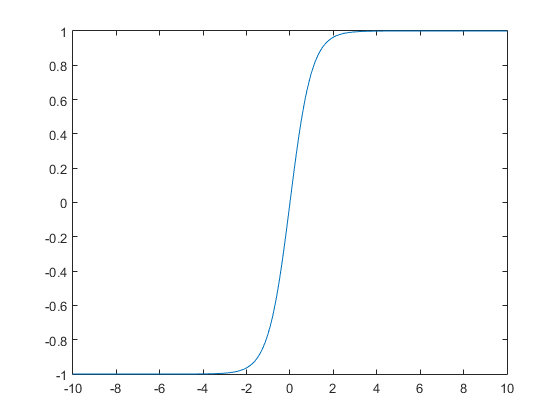

tanh(4) = (exp(4)-exp(-4))/(exp(4)+exp(-4)) = 0.9993
超过[-4,4]的范围已经可以看为1了。
双曲正切函数的标准导数公式:
$$ tanh(x) = \frac{1}{cosh(x)^2} = 1- tanh(x)^2 $$
用如下命令作图,并画出导数图像:
plot(x,1-tanh(x).^2)
plot(x,1./cosh(x).^2)
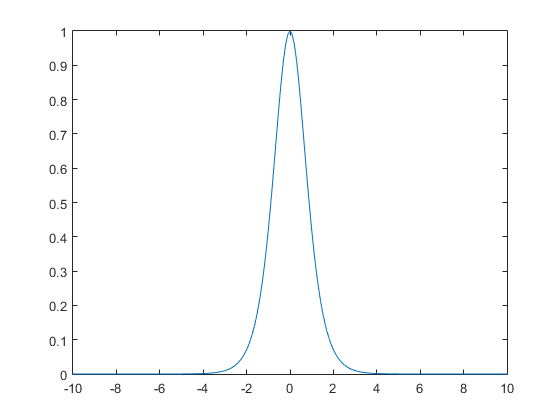
代码中给出的导数公式为:
$$f’_{tanhx} = 1.7159 * \frac{2}{3} (1 -\frac{1}{1.7159^2}tanhx^2) $$
用如下命令plot(x,1.7159*2/3*(1-1/1.7159^2*tanh(x).^2))作图,画出导数图像:
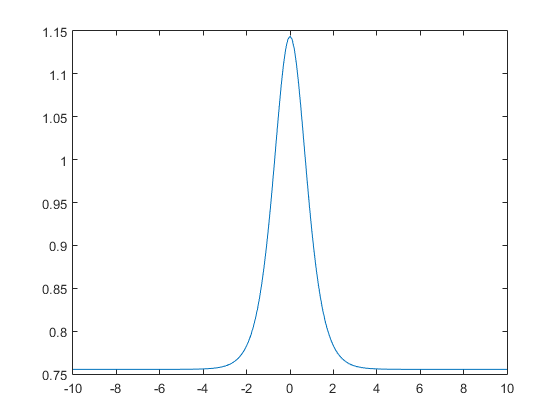
可以看到,总体形状是类似的,但是幅度上还是存在着较大差异。具体缩放的原因还不太清楚。
总结
这篇文章只要是基于公式推导BP网络的整体流程。基于代码的实现请参阅: DeepLearnToolBox之BP算法。


